از دکتر ن. واحدی

سخن نویسنده : پایه هر نظام سیاسی منطبق بر فهم عمومی است. ازاین رو پیشرفت با بالا رفتن فهم عمومی میّسر می شود. این مقاله سعی دارد به این مهمّ کمک نماید.

مسئله “وحدت وجود” سرآغازی چند هزار ساله دارد. “تالس“Thales  بنیانگذار مدرسه “میلت”[1] Milet (در کرانه شرقی دریای مدیترانه، ترکیه امروز)[2] حدود 600 سال پیش از میلاد مسیح شاید اولّین کسی است که در پی یافتن “علّت نخستین” (یا «آرشه»)  Archeپیدایش جهان است. او پس ازمطالعات زیادی عنصر “آب” را مسبب اساسی آفرینش دنیا می­داند و می­گوید :

” آب چشمه همه چیز است و همه چیز دوباره به آب برمی­گردد”[3]

متنی که به زبان عربی حدود 2000 سال بعد :

« انا لله و انا الیه راجعون»

به معنی : “همانا ما از آن خداییم و به سوی او  باز  ‌می­گردیم”

(بخشی از آیهٔ ۱۵۶ سورهٔ بقرهٔ قرآن) قرائتی دیگر پیدا می­کند. با این تفاوت که حالا به جای “آب”  کلام “الله”  نشسته است.

به هرحال اندیشه “تالس” را شاگردش “آناکسیماندر” Anaximander[4] کامل نمود و به شکل زیر ارائه داد:

“نامتناهی علّت نخستین است؛ چیزها یا آغازند(یعنی اصل­اند) و یا این که آغازی را سبب می­شوند. اما آنچه نامحدود است آغازی ندارد. زیرا در غیر اینصورت آن آغاز برایش حّد می­شود. همین طور آنچه علّت نخستین است خودش ایجاد نشده است، او ابدی است (از بین رفتنی نیست). زیرا هرچه بود شود باید ضرورتأ نابود گردد مانند هر معبری که می­بایستی انتها داشته باشد. پس آغاز(اصل) شروعی ندارد. بلکه به نظر می­رسد که خودش آغاز همه چیزهای دیگر است، فراگیر و مهار کننده­ی همه­ی فرآیندهاست. ”

آناکسیماندر جوهر(نامتناهی یا آپیرون Apeiron) را اصل نخستین می­گیرد تا فرآیند “شدن” هیچ­گاه پایانی نداشته باشد.

“جوهر ابدی(قدیم)است، هیچ­گاه پیری(نقصان) ندارد

و دربرگیرنده­ی همهﻯ کیهان­ها ست”[5]

به علاوه “ حرکت پدیده­ی جاودانی است؛ و با آن کیهان[6] های بیشماری از جوهر به وجود آمده­اند و دوباره به آن بازمی­گردند. این فرآیند که مشروط به وجود حرکت است مدام تکرار(دنیا تظاهر وقایع مکرر است) می­شود[7]. پس علّت به وجود آمدن و از بین رفتن هر چیزی جوهر است”[8].

آنچه آناکسیماندر در این سخنان که جلوه دیگری از اندیشهﻯ اوست، بیان می­دارد عاری از هر گونه متافیزیک و تنها محصول عقل ناب است. عقلی که در بند هیچ قیدی نیست. اما چه در دوران باستان و چه به هنگام ایجاد ادیانِ سامی، از جمله اسلام، این سخن که سخن عقل است با همان معنایی ­که آناکسیماندر به آن داده به عمد متافیزیکی تعبیر شده و همان ­طور که تاریخ نشان می­دهد طی هزاران سال سد توسعه­یِ علم گردیده است.

نه تنها این، بلکه کلام “کیهان” که برای نخستین بار به وسیله “فیثاغورث”[9] به کار برده شده، در ادیان سامی نیز وارد شده است. با این تفاوت که کیهان در نزد دین سالاران برآمده از ” امر خلق” و در نتیجه صورتی جادوئی است. اما بایستی دانست که این صورت جادوئی نه برگرفته از اندیشه­های آناکسیماندر بلکه بازتاب صورتی از خصوصیات خدای مصری “پتاه” Ptah است که حدود هشت هزار سال پیش قدرت و عظمتی در آن دیار داشت. پتاه هر چیزی را که می­خواست خلق کند اسم آن ­را به زبان می­آورد.

به نظر می­رسد که موسی، پیغمبر قوم یهود، چنین خصوصیتی را با خود از مصر به کنعان آورده است. در تورات نیز می­خوانید :

«خدا گفت نور، نور شد»

موسی پیغمبر سنگ نوشته “ده فرمان” خود را نیز که به دستورات “حمورابی Hammurabi”  پادشاه بابل مربوط می­شود از کوه سینائی به صورت بشارت خداوندی به پیروان خود هدیه کرده است.

در این ­جا لازم است توجه خواننده را به نظر آناکسیماندر در باره کیهان جلب کنیم:

آناکسیماندر، برخلاف تالس، پیدایش چیزها را نتیجهﻯ دگرگونی کیفی عنصر نخستین(آب) نمی­داند. بلکه او این پیدایش را حاصل تعادل تضادها می­انگارد که به دلیل پدیده­ی حرکت مدام از نامتناهی تراوش می­کند و تظاهر می­یابد (این­جا باید به مسئله­ی فلوکتوآسیون [10] یا جنبش­های بسیار کوچک توجه کرد که بنیاد انفجار بزرگ است).

به عبارت دیگر جوهر که نامتناهی و پریشیده است، «بود»ها را در اثرجدا شدن «تضاد» ها از هم ایجاد می­کند. بودها محدود، فانی و منظم­اند. ساده­تر نظم همیشه از بی­نظمی کامل پدیدار می­شود. مطلبی که امروز به «کائوس تئوری» معروف است. مثال قابل مشاهده این ادعا را:

• در فیزیک حالت­های پریشیده: پاندول دوبل
• در تئوری جامعه: انقلاب
• در بخش بازار: سقوط اقتصادی

می­توان ملاحظه کرد.

پس، به طور اختصار در باره­ی مدل آناکسیماندر[11] می­توان گفت :

« جوهر، آپیرون، فنا ناپذیر و تولید نشده است»

«این جوهر مدام دنیا سازی می­کند»

جلال­الدین مولوی رومی این مطلب را چند هزار سال بعد زیبا بازگو می­کند:

پس بود دل جوهر و عالَم عَرَض                   سایه­ی دل چون شود دل را غرض

به هر حال اندیشه­ی آناکسیماندر آهسته آهسته یک آئین شد. آئینی که به آن آئین “وحدت وجود” یا پانتائیسم Panthism گفتند.

لازم به یادآوری است که ایجاد متافیزیک به وسیله ارسطو نیز به خاطر یافتن زمینه­اﻯ نظری برای پیدا کردن علّت نخستین و به دست دادن علل ظهور وقایع عالم بوده است.

به واقع مدل فکری آناکسیماندر تأثیر بسزائی در اندیشه­ی فلاسفه و دانشمندان پس از او داشته است. از جمله ارسطو اصل اوّل جهان را حرکت می­داند و صفات جوهر (نامتناهی) را در خدا می­انگارد. به علاوه همان ­طور که می­دانیم الهیات ادیان سامی همه منبعث از تفکر ارسطو هستند. همین ­طور تفکر کیهانی ژردانو برونو (پانتائیست) از آناکسیماندر گرفته شده است که از یک ­سو بیان انگارهﻯ ” تک بنی” بودن عالم هستی و از سوی دیگر همریشگی انسان و همه­ی جهان با نامتناهی است. از این­ جا معلوم می­شود که منصور حلاج هنگامی که فریاد می­زند “اناالحق” درهمین متن می­اندیشده است؛ و حرکت جوهری ملا صدرا (صدرالدین محمد بن ابراهیم قوام شیرازی) متأثر از حرکت جاویدان جوهر، یعنی آپیرون، است و بالاخره تعریف نیچه از تاریخ به واقع همان “ آمدن مکرر وقایع” آناکسیماندر است.

در میان عرفای ایرانی “وحدت وجود” به همه خدائی” تعبیر شده است:

همسایه و هم نشین و رهبر همه اوست                        در دلق گدا و اطلس شه همه اوست

در انجمن  فرق    و     نهانخانه  جمع           بالله همه اوست ثم و بالله همه اوست

این تعبیر درخود متناقض است. زیرا مفهوم “خدا” نسبی و تنها در رابطه با دنیا معنی دارد. از این­رو همه خدائی با خود در تضاد است.

جالب این جاست که غزالی در بحث راجع به “جوهر و عرض” یا آنچه به زبان عربی “قدیم و حادث” گفته­اند، براین باور بود که چنانچه اصول منطق (در متن ارسطوئی) را برای آن­ها به کار بریم بدون شک به وحدت وجود (پانتائیسم) می­رسیم. از این­رو غزالی کاربرد منطق را دراین نوع موارد منع می­کند.

اما اگر به یاد آوریم که منطق همانا آئین اندیشیدن است، آن­ وقت به این نتیجه می­رسیم که اندیشیدن در مورد خدا و دین در اسلام ممنوع است. این منع مسئله یکی را در برابر خیلی یا بسیار در پرده­ای از دین یعنی پرده­ای ایراسیونال (Irrational) پنهان می­کند. بنابراین در اسلام مسئله علم و جامعه که هر دو در گروی بحث در باره وحدت و کثرت­اند به فراموشی سپرده می­شوند.

درست به این علّت فیزیکدان معروف آلمان و دارنده جایزه نوبل “ورنر هیزنبرگ  Werner Heisenberg ” ؟،  کتاب خود را ” اجزاء و یکی Teil und das Ganze” نام داده است. اهمیت این گفته در این است که یکی بدون اجزاء (به معنی کثرت) و اجزاء بدون یکی بی­معنی است. در این کتاب هیزنبرگ جهان فیزیکی را چون آناکسیماندر «آرشه» وار می­بیند.

اما آغاز علم ریاضی به عنوان رابطهﻯ اساسی و قابل اندازه­ گیری میان انسان و طبیعت به “فیثاغورث“، فیلسوف مدرسه میلت برمی­گردد که متولّد جزیره “سامک[12] در نزدیکی شهرک “میلت” است. فیثاغورث شیفته اعداد طبیعی، تناسب آن­ها، رابطهﻯ تناسب اعداد با دستگاه موسیقی، نوسانات و حرکات هارمونیک درجهان و وضعیت زندگی بود. به ویژه او اعداد را به اشکال هندسی ربط می­داد. یعنی فیثاغورث اعداد طبیعی را با مجموعه­ای از نقاط مادّی مشابه می­دانست و با کنار هم گذاشتن این نقاط می­توانست به طور زیبائی اشکال اساسی هندسی را بسازد. هم او بود که از عدد 1 و مکرر کنارهم گذاشتن آن همه اعداد طبیعی را ساخت. او از این نمایش که بعدها دمکریت Demokrit  نیز اندیشه اتمی خویش را به وجود آورد، نتیجه گرفت که هر عددی تعیین کنندهﻯ مشخصات اشکال هندسی و با آن چیزهای موجود در جهان است. این نتیجه­ گیری را در ادعای معروف وی می­توان خواند:

“اساس دنیا مادّه نیست بلکه اعداد است”

پس فیثاغورث اعداد را عینی می­پنداشت و آن­ها را حقیقی می­شمرد. هم او بود که می­گفت مشخصات همه چیز به وسیله اعداد تعیین می­شود. حتی فضائل انسان نیز با اعداد هارمونیک مشخص می­گردند. به این شکل او از یک­سو جهان را قابل اندازه­گیری می­کرد و از سوی دیگر پنجره­ای به سوی خرافات باز می­نمود. فیثاغورث برای نظر نخست خود قضیه معروف خویش را (برای تمام مثلث­های قائم­الزاویه و همین طورجمع زوایای یک مثلث 180 درجه است) ارائه داده بود و از سوی دیگر مشخصات هر چیزی را به یک راز عددی مرتبط می­ساخت، اسراری که تنها افراد مُعَّینِی به آن آگاهی داشتند. او بزرگان این افراد را “استاد” می­خواند. با این تصورّ مکتب فیثاغورثیان به وجود آمد که نفوذ بسیار زیادی درکشورهای کرانه دریای مدیترانه پیدا کرد.

اما فیثاغورث هندسه و اعداد را برای خود علوم ریاضی نمی­خواست بلکه او به اعداد به صورت یک راز کیهانی نگاه می­کرد و آن­ها را سنگ بنای این دنیا تلّقی می­نمود. برای او به ویژه عدد 1 تا 10 اساسی و هر یک دارای نیروئی خاص و معنی مُعَینّی بودند. هارمونی جهان ( قبلأ گفتیم که آفریننده کلام جهان فیثاغورث است) از آن­جا ناشی می­شود که همه چیز باهم درتناسب عددی قرار دارند؛ حالتی مشابه آهنگ­های هارمونیک در آلات موسیقی که مثلأ با تقسیم طول تاری که نوسان می­کند می­تواند ایجاد شود.

فیثاغورثیان نخستین گروه ازعارفان جهانند. زیرا همان طور که گفتیم فیثاغورث همه اعداد را (کثرت) تکرار عدد یک می­دانست. یعنی کثرت تکرار وحدت است. مولوی می­گوید :

این محض وحدت است به تکرار آمده

اما در میان اعداد بعضی از اعداد مانند: 1، 2، 3 و7 جادوئی بودند که غالبأ وارد فرهنگ ایران نیز شده­اند. مانند هفت آسمان و هفت ستاره و هفت شهر عشق و یا هفت روز هفته.

تاب آن حسن که در هفت فلک گنجا نیست

جز که آهنگ دل خسته لاغر نکند (مولوی)

فیثاغورثیان معتقد به الیگارشی نیز بودند. از این رو به وسیله طرفداران دمکراسی خیلی زود به شدّت سرکوب شدند. جهان­بینی این مکتب که حرکات جهان را هارمونیک می­دید و زندگی روی زمین خاکی را نیز تنها در شکل هارمونیک مفید و نیک می­پنداشت، روی تصورات قرون وسطی و حتی امروز تأثیر بزرگی گذاشته است.

این تأثیر را امروز در مکاتب عرفانی و لژهای مختلف از جمله فراماسون­ها و در علم و هندسه و معماری می­توان مشاهده کرد. هم اکنون کسانی هستند که برای هر حرفی یک عدد و یا رازی را متصورند و با آن در کتاب انجیل و یا قرآن مجید به دنبال کلماتی می­گردند که تعیین کننده­یِ خصوصیات چیزی است. همین طور معماران قدیم در ساختن معابد، کلیساها و مساجد، اشکال و اعداد ویژه­ای را به کار می­بردند که تنها “استاد” سازنده آن بنا معنی آن­ها را می­دانست (نگاه کنید به معابد هندیان، زردشتیان، بنای کلیساهای بزرگ و یا گنبد مساجد معروف دنیا).

ازاین رو با وجود این که اقلیدس[13] هندسه را به صورت یک علم اصولی ارائه داد، این دانش نه تنها  نتوانست همه دشواری­های موجود روی زمین را حلّ کند، (معمولأ به وسیله مقاطع مخروطی که هنر ریاضیدان یونانی آپولونیوس[14] بود) بلکه رابطه هندسه و اعداد کماکان در هاله متافیزیک باقی ماند.

در میانه قرن هشتم و نهم میلادی ریاضیدانان بزرگ ایران چون خوارزمی و خیام موفق شدند برای موارد معّینی میان هندسه و اعداد یک رابطه برقرار کنند و قفل متافیزیکی هندسه و اعداد را باز نمایند. کلیدی که به آن جبر گفتند. اما اینان در آسمان ریاضی ستاره­ای درخشان نشدند. زیرا کارشان نه عام بلکه خاص بود. لذا رابطه هندسه و اعداد بُعد جادوئی خود را کماکان حفظ کرد.

بدون شک این گرفتاری برآمده از گمراهی فلسفی ارسطو بود که جهان ” تک بنی” آناکسیماندر را به دنیای” دوبنی” “جان و تن” مبدّل ساخته بود. این گونه جهان­بینی چون موازی جهان­بینی ارائه شده در تورات بود، در ادیان سامی جا باز کرد و هزاران سال گسترش دانش آدمی را از جمله برطرف ساختن جادوئی بودن رابطه هندسه و اعداد، به تعویق انداخت. اهمیت این رابطه عملأ به گفتار فیثاغورث بر می­گردد که دنیا را دنیای اعداد می­دانست. به بیان دیگری که با فهم امروز بیشتر سازگاری دارد، فیثاغورث روابط موجود در جهان را روابطی خرد گرا می­دید و به طور کلّی باید گفت : خردگرائی جهان یعنی دنیا دنیائی قابل محاسبه است.

ازاین رو قرن­ها بایستی سپری می­شد تا به مدد جنبش انسان­گرائی و اکتشافات علمی کپرنیک و گالیله قدرت و هیبت کلیسا شکسته می­شد تا در قرن هفدهم کسی چون “رنه دکارت” نه تنها با محور مختصات کارتزی – عمودی خویش طلسم متافیزیکی رابطه­ی میان هندسه و اعداد را درهم شکست بلکه مضافأ جلوه­ای از خردگرائی دنیا را(راسیونال بودن) ترسیم کرد. به علاوه در محور مختصات دکارت همه چیز تنها در تناسب با یک مبداء (ناظر) قابل مشاهده می­شد. این موضوع به این معنی است که  معرفت آدمی با تشخیص یک اختلاف یک ” دیفرانس” به دست می­آید. به ویژه این اختلاف را می­توان روی یک منحنی و یا مسیر حرکت یک جسم به وسیله دونقطهﻯ متفاوت از هم (یا دو زمان مخالف در روی مسیر حرکت) نشان داد و این فاصله را تا آن­جا که ممکن می­شود کوچک  کرد و حتی به نزدیکی صفر برد(میل به صفرکرد). معرفت حاصله از این کار(مماس منحنی در نقطهﻯ معینیّ یا مشتق یک فونکسیون درآن­جا) تفکردکارت را به سوی هندسه تحلیلی برد. آنچه که تبدیل هندسه به معادلات جبری بود. آنچه که کمر متافیزیکی اعداد را شکست و تحقق اشکال و اشیاء جهان را در رابطه با معادلات جبری کرد.

در نتیجه بلافاصله در قرن هفدهم و هیجدهم میلادی کسانی چون نیوتن و لایب نیتس پیدا شدند که همزمان براین مبنا حساب با اعداد بسیار کوچک را عنوان ساخته و با آن معادلات دیفرانسیل را برای حرکت اجسام به طورعام (یونیورسال) ارائه دادند. این معادلات نه تنها محلی (تابع محور مختصات) بودند بلکه دنیا را نیز علّی یعنی “علّت و معلولی” منظور می­کردند. این نگاه به خوبی تأثیر و نفوذ جهان بینی دینی را معلوم می­کند که دنیا را دنیائی قدیم می­پندارد.

بنابراین درآغاز قرن بیستم با وجودی که علم و فن برپایه مکانیک نیوتنی پیشرفت­های چشمگیری داشت معذالک دوعیب اساسی را در خود پنهان داشت. یکی علّت و معلولی بودن جهان و دیگری وجود ناظری که بر عین اثر نمی­گذارد.

به طور کلّی معادله حرکت نیوتن رابطه­ای عام است؛ بیانی ریاضی برای پدیده­ها و اتفاقات طبیعت است؛  کلامی که انسان را توانا می­سازد با صدف دنیای اطراف خویش گفتگو کند. سعدی در زمان خودش این مطلب را بنابر دانائی آن روز چنین توصیف می­کند :

برگ درختان سبز در نظر هوشیار                هر ورقش دفتری است معرفت کردگار

توجه بفرمائید که در قرن هیجدهم میلادی آنچه نیوتن بر روی کاغذ می­آورد توصیف اندیشه کردگاری آناکسیماندر است. یعنی آنچه از “کوزه آپیرون” به بیرون تراوش می­کند نه تنها مشمول :

“ازکوزه همان برون تراود که دراوست” بلکه حرکت آن چیز نیزدر بند قوانینی است که بنیاد آن کوزه

است”

به عبارت دیگر گفتگوی نیوتنی گفتگوئی مستقیم (با زبان ریاضی) با طبیعتی است که چیزهای درونش همه بر مبنای معادله نیوتن حرکت می­کنند. این حرکت، حرکتی در فضای زمان – مکان است(با مختصات دکارتی یعنی کارتزی). از جمله می­توان آن­را برای حرکت جسمی در فضای سه بُعدی مکانی و تک بُعدی زمانی تصور کرد. بدیهی است که این معادله قابل تعمیم به فضاهای n-بُعدی (n عددی طبیعی) نیز هست (مانند حرکت اجرام سماوی و یا حرکت مولکول­های یک گاز).  دراین فضاها یکی از مهم­ترین مسائل مسئلهﻯ پیداکردن برآیند نیروهاست. ولی دراین محاسبه بایستی از خصوصیات هندسه اقلیدسی استفاده کرد. اما دانشمندانی در قرن نوزدهم آمدند و به تأمیم اصول هندسه اقلیدسی (که برای سطح، یعنی فضای دوبُعدی نوشته شده) به فضاهای بیش از دوبُعد، ایراد گرفتند. تازه در روی سطح زمین نیز که بخشی از یک کره می­باشد نمی­توان هندسه اقلیدسی را به کار برد. به ویژه اندازه گیری­هائی که روی زمین صورت گرفته براین ادعا صحهّ می­گذارند. به این جهت در قرن نوزدهم میلادی گوآس، “لابوچوسکی” و “بولیائی” نشان دادند که هندسه اقلیدسی تنها هندسه­ای نیست که در خود بی­نقص است. بلکه امکان وجود سیستم­های دیگری به این سیاق نیز وجود دارد. آن­ها این هندسه را هندسه غیر اقلیدسی گفتند. بالاخره چنین هندسه ای به وسیله ریمان و هیلبرت د(راواخر قرن نوزدهم) به وجود آمد. اما می­بایستی متذکر شد که دراین گونه هندسه­ها اصل خطوط موازی اقلیدس(اصل پنجم) صادق نیست.

درست هندسه سطح کره زمین، نقشه برداری روی آن و خطوط جغرافیائی برای دریانوردی و کوک کردن ساعت نسبت به ساعت معیّنی درمحل خاصی، بخش عمده­ای از دشواری­های دوران گوآس بودند. زیرا درآن زمان معلوم شده بود که روی سطح کره در فواصل نزدیک (محلی یا Local) هندسه اقلیدسی، و برای فواصل دور هندسه غیراقلیدسی صادق است. به این جهت نقشه برداران کره زمین را به بخش­هائی محلی قسمت کردند که بنابرهندسه اقلیدسی قابل انتقال به روی یک صفحه کاغذ است. این کاغد را یک کارت یا ورق گفتند. حالا می­شد ورق­ها را نسبت به یک نقطه مشترکی پهلوی هم گذاشت. به این شکل کره زمین بر روی یک صفحه دو بُعدی مسطح نقش می­یافت که همین نقشه جغرافیائی امروزی است (شباهت این کار با ایجاد سطوح ریمانی به خوبی دیده می­شود) . چنین کاری به زودی نام  “توپولوژی” به خود گرفت. شکل زیر این دشواری را نشان می­دهد.

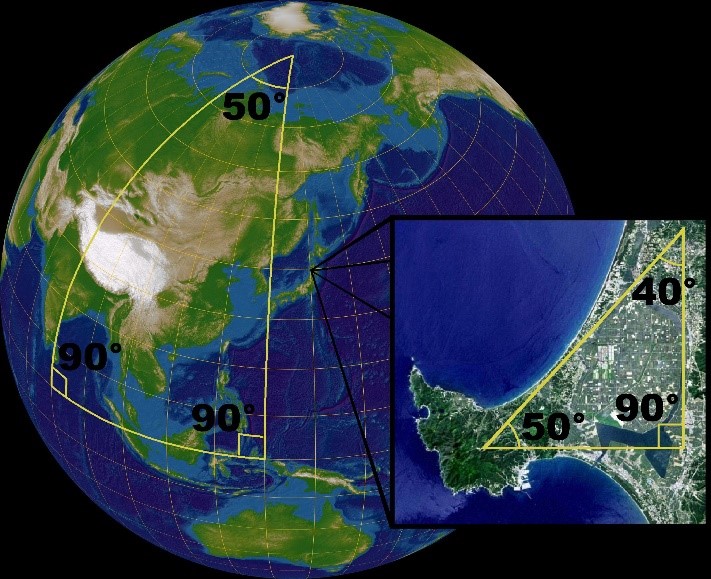
هندسه در روی کره زمین و طرز ترسیم آن بر روی یک صفحه کاغذ

این چند سطر در باره تحول در علم هندسه لازم بود تا بتوان علّت پیدایش نظرات انتقادی در علوم طبیعی و به ویژه ریاضی را در اوایل قرن بیستم روشن کرد.
در این دوره که دوران مکتب نومثبتیون است، مکتبی که نه تنها منطق را جان تازه¬ای بخشید، بلکه با توجه به انتقادات موفقی که به هندسه اقلیدسی شده بود اصول اساسی علم ریاضی را سخت به انتقاد کشید.
تمام بحث¬هائی که در این چند صفحه آورده شد تنها به این منظور بود که معلوم کنیم فزونی دانش و گسترش آن بدون انتقاد ازآنچه که هست و تردید در درستی آن¬ها، خواه در جامعه و سیاست، خواه در علم و ریاضی و فلسفه، هرگز نمی¬توانست نوآوری و پیشرفت حاصل شود.
یعنی تفکرارتجاعی، مسیر حماقت و نادانی را هموار و اندیشه مترّقی شناخت کهنه ها و فاصله گرفتن از آن¬ها را کیلومتر شمار پیشرفت و توسعه می¬سازد.
بر اساس این حکمت نیزکارهای جدید ریمان و هیلبرت به شدّت پایه¬های اساسی ریاضی را به لرزه درآورد. به ویژه پایه¬های سیستم¬هائی که بر مبنای «اصول» به وجود آمده بودند(مانند هندسه، متافیزیک و دین) به لرزه درآمد. چه در فضائی که مکتب نومثبتیون به وجود آورد هراصلی (درهر فکری و باوری) می¬بایستی برگواهی تجربی و نه متافیزیکی استوار باشد. معروف-ترین کسی¬که پرچمدار این راه شد هانری پوآنکاره بود. این فیلسوف و دانشمند فرانسوی صحّت مطلق اصول ریاضی را جایز ندانست و گفت این¬ها فقط به خاطر ساده کردن مسائل آورده می¬شوند. یعنی انتخاب آن¬ها به طورمصلحتی صورت می¬گیرد. در مورد قوانین طبیعت درفیزیک نیز “امیل بوتروکس”[15] برای نخستین بار کلام اقتضائی[16] را بکار می برد.

“قوانین طبیعت نه الزامی بلکه همه اقتضائی (به گونه دیگری هم ممکن بود باشند) هستند”.

معروف¬ترین کسانی¬که مکتب نومثبتیون را که قبل از جنگ اوّل بین¬المللی به وجود آمده بود تشکیل می¬دادند عبارتند از :
« هانس هان، اتو نویراد، رودلف کارناپ، کورت گودل، آلفرد تارسکی، هانس رایشنباخ، لودویگ ویتگن اشتاین، کارل پوپر، ارنست ماخ، دیوید هیلبرت، هانری پوآنکاره، کوتلوب فرگ، برتراند راسل»[17]
بعلاوه ارنست ماخ فلسفه را به انتقاد کشید تا جائی¬که کسی چون وایت هد[18] به فلسفه رنگ و روی جدیدی داد.
در بخش فیزیک هلمهولتس[19] با توجه به این که غلط بودن اصل پنجم هندسه اقلیدسی( اصل خطوط موازی) ثابت شده بود به طور کلّی اصول آپریوری را(وجود چیزهائی پیش از تجربه، چون زمان و مکان) رد کرد.
درمورد اعداد ریشارد ددکیند[20] و جزف پیآنو[21] سیستمی را به وجود آوردند که قدرت تفکر و خلاقیت آدمی را به بهترین وجهی آشکار می¬سازد. آن¬ها نه تنها حساب با اعداد را به کمال رسانیدند و آن را از سیطره عرفانی فیثاغورث درآوردند بلکه ساختارهای عددی جدیدی را ممکن ساختند که نبوغ تفکرانتزاعی آدمی را متجلی می¬سازد. ناگهان دنیا شاهد ساختارهائی به نام “سیستم”، “کلاسه”، ” گروپ”، “پیکر”، “حلقه”، ” بردار”، “ماتریس”، “تانسور”….. شد. حالا این مفاهیم جدید علم ریاضی بیانگر رموزی عددی بودند که فیثاغورث به آن¬ها باور داشت. از جمله تانسورها که به نظر آلبرت انشتاین بیان خمیدگی فضاهستند، به واقع حامل ضرورت حرکت اجسام کیهانی و انتشار نور در کهکشان¬ها می¬باشند. یعنی همه چیز مقید به این خمیدگی است، خمیدگی¬ای¬که علم ریاضی را به صورت یک راز، به صورت یک طلسم بر گردن کیهان نهاده است.
بالاخره مهم¬ترین کاری که در نیمه دوّم قرن نوزدهم صورت گرفت ایجاد “سیستم مجرد فکری” به صورت علائم و “جبر بول”[22] بود. کتاب ژرژ بول به نام ” قوانین تفکر” نشانه عظمت اندیشه¬ایست که ماکسئول (به هنگام پیدا کردن معادلات الکترو مغناطیسی خود) آن را خدائی دانست.
دستگاهی را که ژرژ بول به طور مجرد و به صورت علائمی چون x, y, z,…. برای فکر و کار ریاضی و رابطه میان آن¬ها ارائه داد نه تنها یک بنوغ است، نه تنها بدون آن¬ها امروز علم ریاضی چنین وسعتی را نداشت بلکه نشانه ایجاد زبانی ریاضی است که قدرت و وسعت آن به اندازه¬ی نه این کیهان بلکه کیهان¬های ممکنه بسیاری است.
امروزه این جبر در تمام مدارهای الکترونیک، داده پردازی¬ها و سیستم¬های مخابراتی و مهار جریان¬های خودکار و دستگاه-های ارتباط جمعی و بالاخره در تکنولوژی کاربرد دارد.
در کنار این¬کار فیلسوف و ریاضیدان آلمانی “گوتلوب فرگ”[23] مخترع منطق نمادین یا سمبلیک است. فرگ از خود کتابی به نام “الفبای مفاهیم”[24] به جای گذاشته است که درواقع بیان تفکر ناب به صورت “حساب به زبان فورمولی” است. مانند :
جمع دو عددو حاصل آن : یعنی a+b = c
فرگ با این کار و به هنگام تهیه کتاب “حساب به صورت فورمولی” خود در می¬یابد که نوشتن مسائل هندسه و حساب و یا به طور کلّی تهیه کتاب تخصصی با استفاده از زبان معمولی ممکن نیست. او این دشواری را دشواری رابطه میان کلام و واقعیت¬ها تشخیص می¬دهد.
اما اگر عمیق نگاه شود این دشواری به ارتباط میان ریاضی، منطق ، شناخت و روانشناسی برمی¬گردد که درواقع مراحل درک آدمی از واقعیتی را تشکیل می¬دهند.
فرگ با تشخیص لزوم رابطه¬ای خردمندانه میان کلام و واقعیت¬ها (انسان و جهان)سبب فعالیت وسیع رودلف کارناپ در ایجاد زبانی علمی شد که امروز به نام متا زبان[25] معروف است.
به علاوه دکارت با اصول فلسفی خویش درواقع پایه¬های اندیشه¬های فلسفی را در سیستم بیداری انسان (جان) آشکار ساخت. این کوشش به همراه انتقاد ماخ و نوشتار ” فلسفه به صورت علم دقیق” نوشتهﻯ ادموند هوسرل (به سال 1911) باعث شدند تا رودلف کارناپ فلسفه¬ای علمی درنوشته معروف خویش به نام ” ساخت منطقی دنیا” به دست دهد.

رودلف کارناپ و کارل پوپر که از اعضای مکتب وین بودند مشوق اصلی تعریف دانش در قرن بیستم شدند :
“دانش یعنی سخنی که ضروت آن منطق است. به عبارت دیگر هرکسی می¬تواند بر پایه فرضیات اساسی یک دانائی (علم) و مراحل فکری آن بدون شک خود نیز آن را ذهنأ استنتاج کند. به این شکل دیگر جائی برای نظرات شخصی باقی نمی¬ماند.
از این¬جا می¬توان تاتولوژی (تکرارواضحات) را به صورت “اگر p پس p” و تضاد منطقی را در شکل ” اگر p پس p͂” نوشت (p͂ یعنی نفی p).
به ویژه می¬بایستی توجه داد که کارناپ منطق اندوکتیو را به وجود آورد تا از تضاد منطقی جلوگیری کند.
اما :
تا به حال سعی شد نشان داده شود که هندسه و اعداد در گسترش و تکوین علم نقش اساسی داشته¬اند. به ویژه هندسه ترسیمی و انحناء که دنیاهای مختلفی را به وجود آورده¬اند از اهمیت فوق¬العاده برخور دارند. به خصوص فضاهای متریک یا فضاهائی که در آن¬ها اندازه¬گیری تعریف شده است، در علوم طبیعی درکانون توجه قرار دارند.
“از قرن 19 به بعد رشتهﻯ “توپولوژی”، رشته ¬ای از ریاضی، اهمیت پیدا کرد”قبلأ توپولوژی برای کارهای ویژه¬ای از هندسه و مسائل تحلیلی به کار رفته بود. ازجمله برای مسئله¬ای¬که اویلر در شهر “کونیگزبرگ” (در پرووس یا در لهستان امروز) مطرح ساخته بود.
در این شهر روی رودخانه “پرگل” هفت پل وجود داشت.

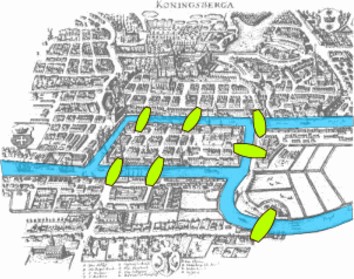
پل¬های روی رودخانه پرگل در “کونیگزبرگ”

اویلر می خواست ببیند آیا می¬توان بدون این که دوبار از روی این هفت پل عبورشود یک دور گردش را به پایان رسانید. او برای پاسخ به این پرسش از روش توپوگرافی استفاده کرد و برای این مسئله گراف زیر را ترسیم نمود( البته ریمان بعدأ برای حلّ این مسئله از معادلات جبری استفاده کرد) :

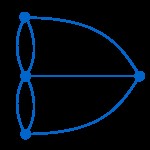
Königsbergگراف برای مسئله یک دور گردش بر روی پل¬های پرگل” در شهر

این گراف نشان می¬دهد که در مسائل توپولوژیک برخلاف هندسه حفظ شکل اهمیت ندارد، بلکه درکانون توجه خصوصیاتی قرار دارند که در تغییرهمگانی دلخواه (دفرماسیون) پایدارمی¬ماند. بنابراین چون شکل یک فنجان می¬تواند به یک تیوب دوچرخه تبدیل شود این دو از نظر توپولوژیک برابرند. درحالی که چنین برابری با یک کره نمی¬تواند برقرار شود. زیرا در مورد کره هر منحنی بسته¬ای را می¬توان به یک نقطه تبدیل کرد. در صورتی¬که این¬کار با یک فنجان ممکن نیست(اگر از دسته آن بخواهد بگذرد).

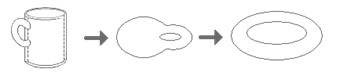
تغییر شکل از فنجان یه تیوب دوچرخه

پس ملاحظه می¬شود که منحنی¬های بسته خصلت خود را در تغییر شکل همگانی(دفرماسیون) حفظ می کنند، آن¬ها اینواریانت هستند. پوآنکاره این خصوصیت را بعد به سطوح سه بُعدی نیز تعمیم داد.
به طور کلّی در مجموعه اعداد کامل می¬توان عملیات جمع و ضرب کرد. در ریاضی به چنین مجموعه هائی حلقه گویند. اما چنانچه به جای اعداد کامل مجموعه¬های مختلفی را اختیار کنیم و برای این “مجموعه از مجموعه¬ها “عملیاتی نظیر جمع و ضرب ممکن باشد به آن توپولوژی گویند.
امروزه توپولوژی همه جا مورد استعمال دارد. از جمله در فیزیک ذرات بنیادی، بخش نظریه ریسمان[26] در شکل فضاهای مدولار و در شیمی مولکولی در شیرالیتی[27] اتم کربن جلوه خاص خود را دارد.

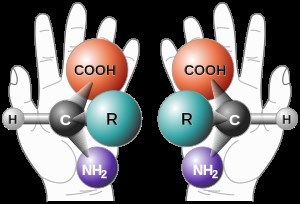
شیرالیتی)تفاوت آئینه¬ای) عنصر کربن در مولکول Amino Acids

سخن پایانی :
در طول این مقاله سعی کردیم درجات و مراتب علم ریاضی و تحّولات آن¬را به نمایش بگذاریم و میان درجات و مراتب تفاوت قائل شویم. این تفاوت درست حکمتی است که در اختلاف کار انتزاعی و غیرانتزاعی(موردها) نهفته است. ازاین رو باید انتظار داشت دانشمندان ایرانی را نه بر مبنای یک علاقه خاص بلکه برپایه مرتبه و درجه علمیشان ارج گذاشت و آن¬ها را معیاری برای فرهگ و دانش کشور دانست. در این راه هرگونه امامزاده سازی مسلمأ جامعه را به نابخردی می¬کشاند.
کتاب شادروان مهران باستی زیرعنوان DNA of Mathematics بیانی از ژرفای دید فلسفی – ریاضی کسی است که دنیا را از زاویه “وحدت وجود” می¬نگرد. زنده یاد دکتر مهران باستی به درستی می¬گوید اگر ردپای وحدت وجود در فیزیک با بیگ بنگ و یا در بیولوژی با DNA ارائه می¬شود، مسلمأ این وحدت دارای بیانی ریاضی نیزهست. زیرا طبیعت شرح شدن¬ها و احوال خود را با قلم خویش(که قلم ریاضی است) دراین سپهرکبود نگاشته است. لذا آنچه فیزیک و یا بیولوژی به زبان ریاضی ارائه می¬دهد بایستی جزئی از یک دنیای ریاضی باشد. اما دنیای ریاضی را نیز می¬بایستی با یک فرمول ریاضی آفرید. شادروان باستی این فرمول را نیزبه دست می دهد. بخش اساسی این آفرینندگی ریاضی سیستم¬های خودسازمان¬دهنده هستند که ضمنأ خودنگر و خود تشریح گر[28] اند. چنین کاری یک کار انتزاعی است.
در امریکا خانم “مریم میرزاخانی” پس از تکمیل دانش ریاضی خود به مسائل “سطوح ریمانی” کشش یافت که برای اولین بار در آلمان مورد علاقه “گوآس”[29] و بعد شاگرد وی ” ریمان”[30] قرار گرفت.
سطوح ریمانی بر می¬گردند به دشواری¬هائی که توابع چند مقداره به همراه خود می¬آورند. مانند توابع تناوبی (سینوس و کوسینوس) و یا توابع لگاریتمی. این توابع همه جا دارای تابع معکوس نیستند. هنر ریمان در این است که می¬تواند سطوحی را بسازد که روی آن (سطوح ریمانی) توابع تناوبی یا لگاریتم تابع معکوس نیز دارند. مثال برای سطوح ریمانی غنچه گل سرخی است که تا بسته است تمام گلبرگ¬هایش درهم انباشته شده¬اند و نمی¬توان آن¬ها را ازهم تفکیک کرد. اما اگر این غنچه شکفته گردد آن¬وقت هر گلبرگی درعین تفاوت داشتن با گلبرگ¬های دیگر در یک نقطه (ساق) به هم وصل¬اند. ریمان هم بخش-هائی که در آن¬جا مثلأ تابع لگاریتم تابع معکوس دارد (یک گلبرگ) ازهم متمایز می¬کند و آن¬ها را پهلوی هم می¬گذارد و در یک نقطه به هم سنجاق می¬کند.
آشکار است که بررسی ساختارهای ریاضی روی سطوح ریمانی نیاز به دانائی وسیعی در بخش¬های مختلف ریاضی و توانا بودن به آن¬ها را دارد. این بخش¬ها عبارتند از : تئوری گروپ، گروپ¬های آبلی، گروپ¬های سوپرتقارنی، گروپ¬های آفین و توپولوژی.
پس ملاحظه می¬شود چنین کاری نه انتزاعی بلکه حلّ مسئله خاصی می¬باشد. متأسفانه ایرانیان مانند همیشه می¬آیند و میان افراد دانشمند خود نیز تبعیض ایده¬ئولوژیک قائل می¬شوند. کاری که یک نوع سنت شده، سنتی که در شکل امام زاده¬ها قابل مشاهده است.

مونیخ: ن. واحدی اوت 2017
مراجع :
[1] مدرسه میلت نخستین مرکزی است که اندیشمندان پیش از سقراط بوجود آوردند تا درآنجا درباره علّت نخستین وجود چیزها، آرشه، علم اخلاق و الهیات به گتگوبه نشینند
[2] لازم به توضیح است که آسیای صغیر، ازجمله شهرک “میلت”(یا میلز) و برخی از جزایر دریای “ایون”، در زمان تالس و حتی تا حدود 500 سال پس از آن جزوخاک ایران محسوب می شده اند
[3] Bruno Snell: Gesammelte Schriften. Vandenhoeck und Ruprecht, Göttingen 1966, P. 119-128
[4] Die Vorsokratiker I : Philipp Reclam, Anaximander, Stuttgart 1999, P.56-974
[5] See 2
[6] Cosmos, see Pythagoras at 7
[7] هزاران سال بعد نیچه نیز این را می¬گوید
[8] See 2
[9] Pythagoras : See 2, P. 98-203
[10] Fluctuation
[11] C. Rapp : Vorsokratiker, München, Beck 1997, S.49.
[12] Samoc
[13] Euclid
[14] Appolonios
[15] Emile Boutroux
[16] Contingency
[17] Hans Hahn, Otto Neurath, Rudolf Carnap, , Kurt Gödel, Hans Reichenbach, Ludwig Wittgenstein, Karl Popper, Ernst Mach, David Hilbert, Henri Poincaré, Gottlob Frege, Bertrand Russell
[18] A. N. Whitehead
[19] Hermann von Helmholtz
[20] Richard Dedekind
[21] Giuseppe Peano
[22] Boolean Algebra
[23] Gotlob Frege
[24] Begriffsschrift
[25] Metat-Language
[26 String Theory
[27] Chirality
[28] self-descriptions
[29] Carl Friedrich Gauß
[30 Georg Friedrich Bernhard Riemann