دکتر حسن بلوری :

فشرده

انسان به تجربه دریافته است که جهانِ هستی قانونمند و قوانینِ سطوحِ مختلفِ آن درهم‌تنیده است. او همچنین دریافته است که دستیابی به قوانین طبیعی از طریق تجربه و آزمایش ممکن است و به‌هیچ‌روی ‌توان تغییر آنها را ندارد.^۲ اما او می‌داند که می‌تواند برای کشف آن قوانین تلاش کند و با تعبیر و تفسیرهای فلسفی از جانب فیلسوفان آشنا با علوم طبیعی به ‌شناخت بهتری از دنیایی که در آن زندگی می‌کند دست یابد. حال این پرسش مطرح است که آیا اصولا برای کشف قوانین طبیعی در چارچوب یک نظریه‌‌ علمی روش یا روش‌های شناخته شده‌ای وجود دارد؟ آلبرت اینشتین در این‌باره در اولین سخنرانی خود در آکادمی علوم پروس، در باره‌ی ’اصول فیزیک نظری‘ می‌گوید:

“در اینجا هیچ روش آموختنی و قابل اجرای سیستماتیک که به نتیجه منجر شود وجود ندارد. پژوهشگر باید آن اصول عام را از طبیعت استراق سمع کند. بدین ‌صورت که او از داده‌های تجربی زیاد مرکب خواصِ کلی معینی را دریابد که قابل فرمولبندی دقیق هستند.”^۳

و در سخنرانی به خاطر شصتمین سالگرد تولد ماکس پلانک، تحت عنوان ’اصول پژوهش‘ می‌گوید:

“کسی که عمیقا خود را با موضوع مشغول کرده باشد نمی‌تواند منکر‌ آن شود که دنیای تمیزدهی و ادراک عملا و به‌وضوح سیستم نظری را تعیین می‌کنند. با این همه، هیچ راه منطقی‌ که از حس‌ها به مبادی و اصول نظری منتهی شود وجود ندارد.”^۴

آن’ اصول عام‘، ’خواص کلی معین‘ و ’قابل فرمولبندی دقیق‘ که اینشتین از آنها صحبت می‌کند کدامین هستند؟ آیا می‌توان با ملاحظه‌‌ی آنها از نوعی ’روش دستیابی به قوانین طبیعی‘ سخن گفت؟

تاریخ علم مدرن از دوران گالیله، به‌ویژه از آغاز قرن بیستم، نشان داده است که در اکثر موارد چنان امکانی با بهره‌جوئی از مفهوم‌های’تقارن (Symmetry)‘،لاگرانژین (Lagrangian) و ’قضیهِ نوتر (Noether’s theorem)‘ وجود دارد. دستاوردهای بیشمارِ نظریه کوانتوم و نظریه نسبیت بخوبی درستی این ادعا و کارائی چنان روشی را نشان می‌دهند.   

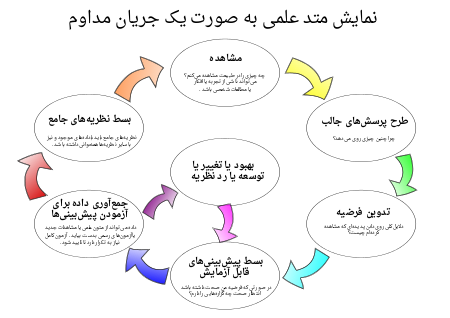
در این مقاله کوشش می‌کنم نشان دهم که بسیاری از قوانین (بنیادین) طبیعی با بهره‌جوئی از مفهوم‌های نامبرده و فرمالیسم لاگرانژی در راستای بیانات ذکر شده از اینشتین امکان‌پذیر است.
توجه داشته باشیم که در اینجا سخن از کسب قوانین علمی به‌معنای فراگیریِ نتایج پژوهش‌های ارائه شده و حاضر و آماده، نیست. بلکه بحثِ روشِ علمی برای دستیابی به قوانین طبیعی، یعنی تولید علم است. متاسفانه در این‌باره در میان ما از آنجمله تحصیل‌کرده‌های دانشگاهی سوء تفاهم بزرگی، اگر نگوئیم غم‌انگیزی، وجود دارد. به این معنا که اکثر ما بین تولید علم و کسب آن از کتاب‌ها و ترجمه‌ها فرقی قائل نیستیم، یعنی معنای علمِ جدید را به‌عنوان ابزارِ تولید علم درنیافته‌ایم.۵

پیشگفتار

به‌طور کلی می‌توان گفت قوانین طبیعی عمدتا به زبان ریاضی، به‌خاطر دقت عمل بالای آن، فرمولبندی می‌شوند. این قوانین بیان از رویدادهای مشاهده (و حدس زده) شده در طبیعت و رابطه‌ی میان آنها، یعنی شیوه‌ی عملکرد طبیعت دارند. در مقاله‌ ’چیستی قوانین طبیعی‘۲ گفتیم: “ما فرض را بر آن گذاشته‌ایم که طبیعت قابل فهم است.” بر این مبنا می‌باید بتوان رویدادهای طبیعی و روابط میان آنها را عینی (objective) فرمولبندی (ریاضی) کرد. اما چگونه می‌توان این خواست را عملی نمود؟
تجربه نشان داده است که لازمه‌ی اجرای چنین خواستی داشتن اطلاعات کافی از پیش‌شرط‌ها و عواملی (عللی) است که سبب بروز رویداد‌ها می‌شوند. اما همین مطلب نیز به آسانی عملی نیست و در اساس به‌ دلیل وجود اصل عدم قطعیت غیرممکن است. طبیعیست که هرچه رویدادها و محیط‌ آنها پیچیده‌تر باشد به‌همان نسبت نیز شناخت از آنها دشوارتر است و بعکس. یعنی، هرچه رویدادها ساده و کمتر با محیط خود تنیده باشند و تجربه و امکانات علمی ـ فنی ما پیشرفته‌تر باشد به‌همان میزان نیز شانس موفقیت در کسب اطلاع از آنها بیشتر است. برای مثال ’سقوطِ آزادِ اجسام‘ را در نظرمی‌گیریم:
مثال: با چشم‌پوشی از تاثیرات محیط در مسئله‌ی ’سقوط آزاد‘، یعنی تصور آن به‌عنوان یک سیستم بسته، ایزوله (در اصل در خلاء)، چهار کمیت قابل شناسایی هستند: ارتفاع (h)، سرعت (v)، شتاب (g) و زمان (t). حال پرسش اصلی در اینجا اینست که به چه طریقی می‌توان چنان رویدادی را علمی بررسی، تشریح و فرمولبندی دقیق (ریاضی) کرد؟ و یا قانون (قوانین) مربوط به سقوط آزاد را کشف و به‌صورت معادله (معادلات) ریاضی ارائه نمود؟ آیا می‌توان در اینجا به مشاهده‌ و برداشت حسی اکتفا نمود و پاسخ درست را دریافت کرد؟
دقیقا در اینجاست که بیانات اینشتین اهمیت و ضرورت خود را نشان می‌دهد:
“… هیچ راه منطقی‌ که از حس‌ها به مبادی و اصول نظری منتهی شود وجود ندارد. … هیچ روش آموختنی و قابل اجرای سیستماتیک که به نتیجه منجر شود وجود ندارد. پژوهشگر باید آن اصول عام را از طبیعت استراق سمع کند.”
و چون ارسطو چنان نکرده بود دچار اشتباه شد. او با اتکاء به حواس می‌پنداشت جسمی که جرم (“وزن”) بیشتری دارد سریع‌تر سقوط می‌کند.
اما پس از گذشت نزدیک به بیست قرن (!) از آن زمان گالیله توانست نه با اتکاء به حواس بلکه با پشتوانه‌ی “از طبیعت استراق سمع کردن” نشان دهد که اندازه‌ی جرمِ جسم کوچکترین تاثیری در سقوط آزاد ندارد. از آن زمان به این طرف انسان در تلاش است که “اعتماد به فکر مجرب نکند بلکه زبان رمزی طبیعت را از اسناد طبیعت، یعنی از واقعیت‌‌های تجربی، بخواند.”۶

گالیله با چشم‌پوشی از تاثیرات محیط، مانند مقاومت هوا، و آزمایش‌های متعدد توانست مسئله‌ی’سقوط آزاد‘ را با‌ قوانینی که مطابقت با عملکرد طبیعت داشت شرح دهد. او به‌طرز عملی، یعنی با پرسش از طبیعت (آزمایش) دریافت که سقوط آزاد نه آن‌گونه که ارسطو باور داشت با مقوله‌ی سرعت بلکه با مقوله‌ی شتاب رابطه دارد! قابل ذکر است که مقوله‌ی شتاب تا آن زمان شناخته شده نبود. یافته‌های گالیله در باره‌ی سقوط آزاد را می‌توان به‌شکل زیر فرمولبندی دقیق کرد:

۱. سرعتِ سقوط (v) یک جسم با طولِ زمانِ سقوط (t) آن رابطه‌ی مستقیم دارد. یعنی، هرچه زمانِ سقوط طولانی‌تر باشد به‌همان میزان نیز به سرعت جسم افزوده می‌شود. این بیان را می‌توان در شکلِ معادله‌ی ریاضی چنین بیان کرد:   v = g t     ( g = 9,81m/s² ضریب شتاب)

۲. ارتفاع سقوط (h) یک جسم با طول زمان سقوط (t) آن رابطه‌ای به شکل معادله gt² h =   دارد. یعنی، تغییر ارتفاع متناسب است با مربع طول زمان (t²). (g شتابِ نیروی گرانشی است که در هر دو معادله در شکل ضریب ثابت ظاهر می‌شود. ثابت به این دلیل که نیروی گرانشی در مکان آزمایش همگن (یکنواخت) در نظرگرفته می‌شود.)

چشم‌پوشی از عوامل تاثیرگذارِ محیط بر سقوط آزاد، یعنی آن را سیستمی بسته یا ایزوله (isolated)  تلقی کردن، سبب کاهش پیچیدگی آن ‌می‌شود. یعنی، تبدیل به سیستمی نسبتا ساده که آسان‌تر قابل بررسی است می‌گردد. در نتیجه مشکل کمتری در کشف، تشریح و بیان رابطه‌ی علت و معلولی آن و ارائه قوانین مربوطه وجود دارد. دقیقا از این‌روست که در بررسی سیستم‌ها همواره‌ سعی بر آنست تا جائیکه ممکن است تاثیرات محیط نادیده گرفته شود. به بیان دیگر، عواملی را که به‌نظر در وحله‌ی اول می‌توان از تاثیرگذاری آنها بر سیستم صرف‌نظر کرد، کنار گذاشت. اما از آنجايیکه هیچ سیستمی را نمی‌توان کاملا از محیط‌ خود ایزوله کرد، معنایش اینست که قوانین بدست ‌آمده نه سراسر واقعی بلکه شکل ایده‌آل دارند.   

واقعی یا ایده‌آل؟

.در مقاله‌ی ’چیستی قوانین طبیعی‘ گفتیم که “ما جهان (گیتی) را نه به‌شکلی که واقعا هست بلکه به‌صورت تقریبی و در شکل ایده‌ال درمی‌یابیم. قوانین طبیعی‌ ارائه شده از جانب ما نمی‌توانند به دلایل مختلف آئینه‌ی تمام نمای طبیعت باشند. از جمله و به‌ویژه به این دلیل که ما اصولا امکان آن را نداریم شرایط اولیه‌ی لازم برای بررسی‌ها را بطور دقیق به‌شناسیم (اصل عدم قطعیت^۷و۸، همدوسی و ناهمدوسی^۹).”^۲

مثالِ ’سقوطِ آزادِ احسام‘ تا حدودی ایده‌آلی بودن قوانین طبیعی ما را نشان می‌دهد. می‌گوئیم تا حدودی چراکه ما تاکنون سوای چشم‌پوشی از تاثیرات محیط چیزی در باره‌ی مرز شناخت خود از کمیت‌ها نگفته‌ایم. این‌که برای مثال ما تا چه اندازه می‌توانیم ضریبِ گرانشی g در معادلات ذکر شده را‌ دقیق شناسایی کنیم؟ بدیهیست که چنین پرسشی تنها محدود به ضریبِ شتاب نمی‌شود بلکه کل کمیت‌های (بنیادین) طبیعی را شامل می‌گردد. پاسخ نظریه کوانتوم به این پرسش کاملا گویاست: اصل عدم قطعیت، یعنی وجود مرزِ شناخت! یعنی، ما توان شناخت کامل از داده‌ها را نداریم. در نتیجه ناچاریم با محدودیت‌ها کنار بیائیم. تنها کاری که در چنین وضعیتی می‌توان کرد اینست که تلاش کنیم دنیای واقعی را با قوانینی هرچند تقریبی (ایده‌آل) به بهترین وجه ممکن، نزدیک‌ به واقعیت، توصیف کنیم گرچه خود در دنیای واقعی زیست می‌کنیم. از این دید، قوانین طبیعی حاضر ابزاری هستند که می‌توانند در آینده با شناخت بهتر از طبیعت دقیق‌تر بیان شوند و یا حتا در حوزه‌های معینی تغییر کنند.^۱۰ بی‌شک جالب و پسندیده هم نیست که نظریه‌های علمی و قوانین طبیعی ما برای همیشه، یعنی بی‌پایان و بی‌حد ومرز معتبر باشند و تجربه نیز نشان داده که چنین نیستند. اگر غیرازاین باشد معناییش جز توقف در زمان نیست. مثال بارز آن نظریه نسبیت عام اینشتین است که اکنون روشن شده در مقطعی به نام تکینگی اعتبار خود را از دست می‌دهد و این هیج تعجبی ندارد. به قول اینشتین هر نظریه‌ای زمانی ’نه‌‘ خود را می‌گیرد.   

مفهوم‌های ضروری

برای بیان و فهم مطالبی که در زیر می‌آیند لازم است کوتاه با چند مفهوم‌ اساسی آشنا شویم:   

کوواریانس یا هم‌وَردایی (Covariance): به تغییرناپذیریِ فرمِ معادلات (فیزیکی) در تغییرِ دستگاه مرجع گفته می‌شود.

ناوَردا یا تغییرناپذیر (Invariance): به ویژگی تغییرناپذیرِ یک کمیت (فیزیکی) در تغییرِ دستگاه مرجع گفته می‌شود.

تقارن یا متقارن (Symmetry): به ویژگی‌ تغییرناپذیر یک سیستم (فیزیکی) در ترانسفورماسیون (تبدیل) گفته می‌شود.  

لاگرانژین (Lagrangian): ایده‌ی اصلی در کسب قوانین طبیعی به حداقل رساندن چیزی به نام لاگرانژین و تعییرناپذیر (ناوَردا) بودن آن در تبدیلی به نام لورنتس است. در غیراین‌صورت ما برای هر دستگاه مرجع‌‌ قانونی متفاوت خواهیم داشت. معنای این گفته آنست که لاگرانژین می‌باید یک اسکالر (Scalar) باشد. اسکالر به ابژکتی گفته می‌شود که در  تبدیل‌های لورنتس تغییر نمی‌کند.^۱۱ این نوع ابژکت‌ها بسیار مهم هستند، زیرا با یاری آنها می‌توان به قوانینی دست یافت که در همه‌ دستگاه‌های مرجع (شاهدان کیهانی) کوواریانس هستند.^۱۱ به لحاظ تاریخی ایده‌ی بهره‌جویی از لاگرانژین ریشه در اصل فرما (یکی از اولین قوانین طبیعی ما) دارد که به‌عنوان یک مثال در مقاله ’چیستی قوانین طبیعی‘بحث کردیم.

فرمالیسم لاگرانژی (Lagrangian formalism): براساسِ ایده‌ی لاگرانژین می‌توان چارچوبی را برای دستیابی به قوانین طبیعی به نام فرمالیسم لاگرانژی (framework called Lagrangian formalism) ارائه داد. به این معنا که با بهره‌گیری از لاگرانژین و اصلی به نام ’اصلِ عمل‘ (Principle of action)”^۲ به قوانینی (معادلاتی) که سیستم (فیزیکی) را توصیف می‌کنند دست ‌یافت. رابطه‌ی لاگرانژین و این قوانین توسط معادله‌ی معروف اُیلر ـ لاگرانژ (Euler-Lagrange equation) بیان می‌گردد.^۱۱ مهم پیدا کردن لاگرانژینِ درستِ مسئله‌ی مورد بررسی است. در زیر به مثال‌هایی اشاره می‌کنیم.

قضیه امی نوتر (Noether’s theorem): قضیه نوتر می‌گوید: هر تقارن لاگرانژی مستقیما با یک کمیت پایدار (فیزیکی) (conserved quantity) مرتبط است.”به کمک فرمالیسم لاگرانژی می‌توان به یکی از مهمترین قضایای فیزیک جدید، یعنی قضیه نوتر دست ‌یافت. این قضیه رابطه‌‌ی میانِ تقارن‌ها (Symmetries) و کمیت‌های پایدار را آشکار می‌کند.”^۱۱ کمیت پایدار (Invariance) به کمیتی (فیزیکی) گفته می‌شود که اندازه‌ی آن در طولِ زمان تغییر نمی‌کند، مانند انرژی.

“به ازای هر تقارن در سیستم (تابعِ متقارن مشتق‌‌پذیر) یک کمیت (فیزیکی) وجود دارد که ناوَردا است.”^۱۲ این مطلب بسیار مهم و شایان توجه است، چراکه کمیت‌هائی که در فیزیک برای توصیفِ طبیعت مورد استفاده قرار می‌گیرند به‌طور مستقیم با تقارن‌ها رابطه دارند. “این رابطه یکی از جالب‌ترین شناخت‌ها در تاریخ علوم طبیعی است.” ^۱۳

قانون پایستگی یا اصلِ بقاء Conservation law)): گزاره‌‌ا‌یست که طبق آن یک کمیتِ مشخص (فیزیکی) در یک سیستمِ مشخص در حینِ تحولِ آن سیستم ثابت می‌ماند. مثال‌های بارز آن اصلِ بقاء انرژی (جرم)، تکانه و یا بارالکتریکی است.

نظریه ذرات و میدان‌ها (بدون کنش و واکنش)

در حال حاضر از دو نظریه برای توصیف پروسه‌های بنیادی در طبیعت بهره‌جسته می‌شود: ۱. نظریه ذرات  و ۲. نظریه میدان‌ها. (تذکر: خصلت محتوای این بخش و بخش بعدی اجازه‌ی ساده کردن بیشتر از آنچه انجام داده‌ام را نمی‌دهد.)

۱. نظریه ذرات سیستم‌های فیزیکی را توسط موقعیت مکانی (t)  ذرات به‌عنوان تابعی از زمان توصیف می‌کند. لاگرانژین در اینجا تابعیست از مکان، سرعت و زمان. مانند  =  m  𝓛،  لاگرانژین معروف فیزیک کلاسیک، کمیتی به نام انرژی جنبشی که در آن  (t)   سرعت ذره و m  جرم ذره است. نقطه بالای    معنای مشتق (t)   نسبت به زمان t را دارند.

 مثال: قانون دوم نیوتن  = m     را می‌توان با یاری لاگراژین   =  m 𝓛   ((- V(  انرژی پتانسیل) و فرمالیسم لاگرانژی بدست آورد. همچنین می‌توان با یاری قضیه نوتر پایستگی انرژی، تکانه، تکانه زاویه‌ای و … را نشان داد. از ارائه‌ی جزئیات مربوطه صرف‌نظر می‌شود. در صورت تمایل می‌توان برای مثال به کتاب^۱۴ مراجعه نمود. همین اندازه اضافه می‌کنم، تا زمانیکه صحنه‌ی عملکرد قوانین طبیعی را فضازمانِ متقارن تشکیل می‌دهد قانون بقاء در مورد کمیت‌های نامبرده صدق می‌کند.^۱۳

۲. نظریه میدان‌ها سیستم‌های فیزیکی را نه با موقعیت مکانی (t)  ذراتِ منفرد بلکه از طریق میدان‌ها توصیف می‌کند. در اینجا نیز فضا و زمان (فضازمان) صحنه‌ی عملکرد میدان‌ نیروی الکتروضعیف^۱۵ ( یعنی، نیروی الکترومغناطیسی و نیروی ضعیف) و همچنین میدان نیروی قوی^۱۵ محسوب می‌شود. لاگرانژین  𝓛  در اینجا تابعیست از میدان, t )  (  ϕ، مشتق آن و مکان..  

مثال: مثالِ معروف لاگرانژینِ (بدون توضیح و صرفا به‌خاطر نمایش ‌‌آن)   = 𝜕𝜇𝛷^†𝜕^𝜇𝛷 – m² 𝛷^†𝛷  𝓛   است. این لاگرنژین در تبدیل لورنتس ناوَرداست و با استفاده از آن در فرمالیسم لاگرانژی می‌توان به معادله ـ کلاین ـ گوردون (Klein-Gordon-Equation) دست ‌یافت.^۱۱ معادله‌ای که امکان توضیح میدان‌های آزاد با اسپین صفر (Spin–0-Fields) را می‌دهد. یعنی، می‌توان با یاری آن سینماتیک میدان‌‌های آزاد اسکالر یا ذراتی بدون اسپین (با یا بدون بارالکتریکی) را تعیین نمود.

معادله‌ی کلاین ـ  گوردون معادله میدان‌ها و یا ذرات با اسپین صفر است که گاهن معادله ـ کلاین ـ گوردون ـ شرودینگر نیز نامیده می‌شود.

“اسپین (Spin, Eigen-Drehimpuls) از خاصیت‌های بنیادیذرات زیراتمی است که معادل کلاسیک ندارد و یک خاصیت کوانتومی به‌شمار می‌آید. نزدیک‌ترین خاصیت کلاسیک به اسپین اندازه حرکت زاویه‌ای است.”^۱۶

معادله‌ی دیراک (P. Dirac) معادله‌ایست نسبیتي‌ و بسیار مهم در تشریح میدان‌های با اسپین    . معادله دیراک از طریق لاگرانژین (بدون توضیح)  =  ( iγ^𝜇𝜕_𝜇 – m)  𝓛_Dirac و فرمالیسم لاگرانژی بدست می‌آید: iγ_𝜇𝜕^𝜇 – m)𝛹 = 0 (.

معادله‌ی  پروکا (Proca Alexander) فیزیکدان رومانی، ۱۹۵۵ـ ۱۸۹۷) یک معادله کوانتوم مکانیک نسبیتی است که خواص ذرات بوزون با اسپین ۱ و با جرم، مانند بوزن W و بوزن Z، را توصیف می‌کند. در اینجا از طریق لاگرانژین مربوطه و فرمالیسم لاگرانژی معادله‌ی پروکا بدست می‌آید. و برای میدان‌های با اسپین ۱ و ذرات بدون جرم (m = 0) مانند فوتون‌ها معادلات معروف (ناهمگن inhomogen) ماکسول حاصل می‌شود.

نکات ذکر شده نشان می‌دهند که می‌توان از طریق لاگرانژین فراخور و فرمالیسم لاگرانژی به قوانین طبیعی دست یافت.

مطالب مزبور مربوط به ذرات و میدان‌های آزاد، یعنی بدون کنش و واکنش‌ میان آنها و با محیط، است. اما همان‌گونه که در ابتدای مقاله گفتیم، یکی از مسائل اساسی در شناخت پدیده‌ها شناختِ چگونگی کنش و واکنش میان آنها و همچنین با محیط است. به‌همین دلیل لازم است در زیر نگاهی هرچند کوتاه به این مطلب مهم با ملاحظه‌ی معادلات ذکر شده و معادلاتی که برهمکنشی‌های مزبور را بیان می‌دارند داشته باشیم، برای مثال برهمکنشی میان الکترون‌ها و فوتون‌ها را. از نگاه نظریه میدان‌ها، کنش و واکنش میان این دو به‌معنای ملاحظه‌ی کنش و واکنش میان میدان اسپین  جرم‌دار با میدان اسپین ۱ بی‌جرم است. برهمکنشی این دو میدان بخش مهمی از فیزیک مدرن تحت عنوان ’کوانتوم الکترودینامیک‘ را تشکیل می‌دهد. بخش توسعه یافته‌ای که در علوم و فنون مختلف کارارایی بسیار فراوان و بالایی دارد.       

نظریه ذرات و میدان‌ها (با کنش و واکنش)

برای دستیابی به قوانینی که برهمکنشي میدان‌های (ذراتِ) مختلف را توصیف ‌کنند نیاز به لاگرانژین‌های متقارن و فراخورِ نوعِ کنش و واکنش‌ها داریم. در اینجا نه مثل بخش پیشین از فضازمانِ متقارن به‌عنوان پس‌زمینه بلکه از ’تقارن‌ درونی‘ سیستم‌های مورد بررسی، معروف به ’تقارن پیمانه‌ای‘ ناوَردا (Gauge theory, Eichtheorie) بهره‎جسته می‌‌شود. ^۱۷و۱۸

در اینجا نیز روش دستیابی به قوانین مربوطه همانی است که پیشتر توضیح دادیم. یعنی، ارائه‌ی لاگرانژین مناسب و متقارن، استفاده از فرمالیسم لاگرانژی (اصل عمل و معادله‌ی اُیلر ـ راگرانژ)، استخراج قانون، استفاده از قضیه نوتر برای ارائه‌ی کمیت‌های پایدار.

دور از تصور نیست که پیدا کردن لاگرانژین‌‌های درست برای چنان پروسه‌هایی کار آسانی نمی‌باشد. بی‌تردید چنان لاگرانژین‌هایی عباراتی را نیز شامل می شوند که مفصل‌تر از تقارن‌های پیشتر ذکر شده هستند. درست به‌همین خاطر از ارائه (حتا نمایش) آنها در اینجا صرف‌نظر می‌شود. در صورت تمایل می‌توان برای مثال به کتاب^۱۹و۲۰ مراجعه نمود. در زیر تنها به ارائه‌ی نکاتی چند در باره‌ی قوانین و مسائل مربوط به این حوزه اکتفا می‌کنم.  

ـ روشن است که توصیف دینامیک ذرات و میدان‌ها (در بنیادی‌ترین سطح) با قوانینی (معادلاتی) که فاکتور زمان را لحاظ می‌کنند میسر است. این قوانین نیز با یاری فرمالیسم لاگرانژی با استفاده از لاگرانژین‌های متقارن بدست می‌آیند.

ـ در برهمکنشیِ ذکر شده میان الکترون (اسپین  ) و فوتون (اسپین ۱) از لاگرانژین متقارن U(1) استفاده می‌شود. پس از انجام فرمالیسم لاگرانژی می‌توان با قضیه نوتر به کمیت پایداری به نام بارالکتریکی دست‌یافت. 

ـ با استفاده از لاگرانژین متقارن SU(2)، برای مثال در برهمکنشی دو میدان با اسپین  مانند میدان الکترون و میدان نوترینو (Neutrino)، و با توجه به نتیجه‌ی آزمایش‌ها که نشان می‌دهند هیچ یک از این میدان‌ها بدون جرم نیستند به این نتیجه می‌رسیم که می‌باید در اینجا اتفاق خاصی معروف به شکستن تقارن SU(2) افتاده باشد.

ـ ایده‌ی شکستنِ تقارن (Symmetry breaking) نقطه‌ شروع سازوکار هیگز ((Higgs mechanism  برای توضیح مکانیزم ایجاد جرم است. در واقع ایده‌‌ی پایه در اینجا استفاده از یک برهمکنشی اضافی با یک میدان (اسپین صفر) به نام میدان هیگز (Higgs field) است. در این‌باره در مقاله^۱۳ می‌خوانیم: “تقارن و شکستن تقارن دو مقوله‌ی بسیار مهم و تعیین کننده برای درک و تشریح کنش‌ و ‌واکنش‌ها در سطوح مختلف طبیعت از ذرات بنیادی تا کل کیهان می‌باشند.”^۱۳

ـ با لاگرانژین،‌ ناوَردای محلیِ با جرم    U(1)و SU(2)  می‌توان نیروی الکتروضعیف، متشکل از نیروی ضعیف^۱۵ و نیروی الکترومغناطیسم، را توضیح داد و در این رابطه با قضیه نوتر به کمیتِ پایداری به نام ایزواسپین (Isospin) که بارالکتریکی نیروی الکتروضعیف محسوب می‌شود دست یافت.^۱۱

ـ با لاگرانژین، ناوَردای محلی که از تقارن درونی یا پیمانه‌ای SU(3) حاصل می‌شود می‌توان نیروی قوی^۱۵ را توضیح داد. اما در اینجا شکستن تقارن اتفاق نمی‌افتد. به‌همین خاطر میدان‌های مریوطه با اسپین ۱ از ذراتی بدون جرم به نام گلوئون (Gluonen) تشکیل شده‌اند.

ـ قابل توجه است که “هیچ چیز در کیهان ما پایدار نمی‌بود اگر نظریه اسپین   به‌همان شکل عمل می‌نمود که نظریه اسپین صفر عمل می‌‌کند.”^۱۱

“یکی از بزرگترین کشفیات در تاریخ علوم طبیعی این بود که طبیعت در بنیادی‌ترین سطح (در دنیای کوانتومی) در تبدیل پاریته (Parity transformation or Parity inversion) ثابت نیست. ابطال پاریته (Parity violation) برای هر فیزیکدانی بدور از انتظار بود. تاکنون هیچکس نمی‌داند که چرا طبیعت چنان غیرعادی رفتار می‌کند.”^۱۱    {\displaystyle \mathbf {P} :{\begin{pmatrix}x\\y\\z\end{pmatrix}}\mapsto {\begin{pmatrix}-x\\-y\\-z\end{pmatrix}}.}

نتیجه

قوانین طبیعی، از آنجمله نیروهای پایه‌ای چهارگانه در طبیعت، را می‌توان با در اختیار داشتن لاگرانژین‌های متقارن و متناسب با حوزه‌ی بررسی، مانند مکانیک کلاسیک یا مکانیک کوانتومی (به‌طور کلی دنیای کلاسیک و دنیای کوانتومی، کیهان)، حاصل از تجربه و آزمایش با یاری فرمالیسم لاگرانزی، یعنی استفاده از’اصلِ عمل‘ (Principle of action) و معادله اُیلر ـ لاگرانژ، بدست آورد و در ادامه با بهره‌جوئی از قضیه امی نوتر که بیان از رابطه میان تقارن‌ها و قوانین بقاء دارد به کمیت‌های پایدار دست یافت.

برلین

۲۰۲۲٫۰۵٫۰۶

مراجع

1. https://fa.wikipedia.org/wiki/%D8%B1%D9%88%D8%B4_%D8%B9%D9%84%D9%85%DB%8C
2. Hassan Bolouri,

۱. حسن بلوری، ’چیستی قوانین طبیعی‘، منتشر شده در سایت‌های فارسی‌زبان، ماه آوریل سال ۲۰۲۲

3. Albert Einstein, Prinzipien der Theoretischen Physik, in: Mein Weltbild, S. 111
4. Albert Einstein, Prinzipien der Forschung, in: Mein Weltbild, Herausgegeben von Carl Seelig, Ulstein Verlag, Frankfurt a. M., Berlin, Wien, 1979, S. 109
5. https://www.youtube.com/watch?v=TbWnebdxI0I
6. Max Born, Experiment und Theorie in der Physik, Physik Verlag, Mosbach/Baden, 1969, S. 37-38; Experiment and Theory in Physics, King’s College in Newcastle-upon-Tyne, 1943
7. Hassan Bolouri, Principle of Causality

۷. حسن بلوری، ’اصل علّیت؟‘، منتشر شده در سایت‌های فارسی‌زبان، ماه ژانویه سال ۲۰۲۰

8. Hassan Bolouri, Causal Asymmetry

۸. حسن بلوری، ’معلول و علت‘، منتشر شده در سایت‌های فارسی‌زبان، ماه می سال ۲۰۱۹

9. Hassan Bolouri, The Concept of Coherence and Decoherence

۹. حسن بلوری، ’مفهوم همدوسی و ناهمدوسی‘، منتشر شده در سایت‌های فارسی‌زبان، ماه دتسامبر سال۲۰۲۰   

10. . https://www.br.de/mediathek/video/alpha-centauri-astro-physik-was-sind-naturgesetze-av:5bd0c6701145970018ec8a69
11. Jakob Schwichtenberg, Durch Symmetrie die moderne Physik verstehen, Springer-Verlag, Deutschland 2017, S. 101, 80, 101,
    12. https://fa.wikipedia.org/wiki/
    13. Hassan Bolouri, Symmetry, the key to recognizing the cosmos

    ۱۳. حسن بلوری. ’تقارن: کلیبد شناخت کیهان‘، منتشر شده در سایت‌های فارسی‌زبان، ماه مارچ سال ۲۰۲۰

    14. Herbert Goldstein, Klassische Mechanik, Akademi. Verlagsgesellschaft, Wiesbaden 1978
    15. Hassan Bolouri, The natural constants and epistemology

    ۱۵. حسن بلوری، ثابت‌های طبیعی و شناخت‌شناسی، منتشر شده در سایت‌های فارسی‌زبان، ماه فوریه سال ۲۰۲۱

    16. https://fa.wikipedia.org/wiki/%D8%A7%D8%B3%D9%BE%DB%8C%D9%86
    17. Roger Penrose, The Road to Reality, Published by Vintage, London, 2005
    18. Helga Baum, Eichfeldtheorie, Springer-Verlag, Berlin Heidelberg, 2009
    19. Michio Kaku, Quantum Field Theory, Oxford University press, New York, Oxford, 1993
    20. Steven Weinberg, The Quantum Theory of Fields I-III, University Press Cambridge, 2005